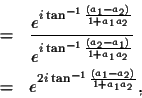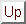

Next: Projective Space
Up: The Projective Plane
Previous: Collineations
Absolute points have a surprising but important application: they can
be used to determine the angle between two lines. To see how this works,
let us assume that
we have two lines
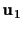 and
and
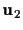 which
intersect the ideal line at two points, say
which
intersect the ideal line at two points, say
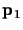 and
and
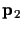 .
Then, the cross ratio between these two points and the
two absolute points
.
Then, the cross ratio between these two points and the
two absolute points
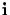 and
and
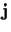 yields the directed
angle
yields the directed
angle 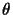 from the second line to the first:
from the second line to the first:
which is known as the Laguerre formula.
To gain some intuition on why this formula is true, let us consider a simple
example. Suppose we have two lines
in the affine plane. It is clear
that these two lines can be represented as two vectors
![$\ensuremath{{\bf v}_{1}} = [1, a_1]^T$](img97.gif) and
and
![$\ensuremath{{\bf v}_{2}} = [1, a_2]^T$](img98.gif) in the Euclidean plane. The directed
angle between the two lines is the directed angle between the two
vectors and is given by:
in the Euclidean plane. The directed
angle between the two lines is the directed angle between the two
vectors and is given by:
Now in the projective plane these lines are represented as
[a1, -1, 0]T and
[a2, -1, 0]T, which are found by mapping points [x,y]T in
the affine plane to points [x,y,1]T in the projective plane.
The ideal line passing through
![$\ensuremath{{\bf i}} = [1,i,0]^T$](img100.gif) and
and
![$\ensuremath{{\bf j}} = [1,-i,0]^T$](img101.gif) is given by
is given by
![$\ensuremath{{\bf i}}\times \ensuremath{{\bf j}} = [0, 0, 1]^T$](img102.gif) .
The two points of intersection between this
line and the two original lines are given by
[1, a1, 0]T and
[1, a2, 0]T. The cross ratio of the four points is then given by:
.
The two points of intersection between this
line and the two original lines are given by
[1, a1, 0]T and
[1, a2, 0]T. The cross ratio of the four points is then given by:
Converting the complex numbers from rectangular to polar coordinates
yields:
from which it follows that
which is the desired result.


Next: Projective Space
Up: The Projective Plane
Previous: Collineations
Stanley Birchfield
1998-04-23
![]() and
and
![]() which
intersect the ideal line at two points, say
which
intersect the ideal line at two points, say
![]() and
and
![]() .
Then, the cross ratio between these two points and the
two absolute points
.
Then, the cross ratio between these two points and the
two absolute points
![]() and
and
![]() yields the directed
angle
yields the directed
angle ![]() from the second line to the first:
from the second line to the first: