Now that we have a representation for lines, we can proceed to more
complex relations. It should not surprise the reader
that the coordinates of the plane passing through the three
points
![]() ,
i=1,2,3, is obtained from the
determinants of the four
,
i=1,2,3, is obtained from the
determinants of the four
![]() submatrices of
submatrices of
![\begin{displaymath}\left[\matrix{
X_1 & X_2 & X_3 \cr
Y_1 & Y_2 & Y_3 \cr
Z_1 & Z_2 & Z_3 \cr
W_1 & W_2 & W_3}\right].
\end{displaymath}](img125.gif)
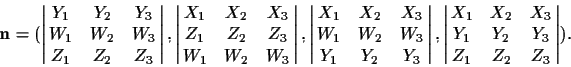
A point
![]() lies on a line
lies on a line
![]() if and only if the vectors
if and only if the vectors
![]() ,
,
![]() ,
and
,
and
![]() are collinear, that is, the
determinants of the four
are collinear, that is, the
determinants of the four
![]() submatrices of the following matrix
submatrices of the following matrix
![\begin{displaymath}\left[\matrix{
X_1 & X_2 & X \cr
Y_1 & Y_2 & Y \cr
Z_1 & Z_2 & Z \cr
W_1 & W_2 & W}\right]
\end{displaymath}](img127.gif)
![\begin{displaymath}A = \left[\matrix{
l_{23} & l_{31} & l_{12} & 0 \cr
0 & -l_...
...& l_{41} & -l_{31} \cr
-l_{42} & l_{41} & 0 & l_{12}}\right].
\end{displaymath}](img129.gif)
Two lines
![]() and
and
![]() intersect if and only if their Plücker
coordinates satisfy the equation
intersect if and only if their Plücker
coordinates satisfy the equation
In this section we have shown how to find the line containing two points and the plane containing three points. Symmetrically, we have shown how to find the point at the intersection of three planes but have not shown how to find the line at the intersection of two planes. This latter problem can be solved by computing the determinants of the submatrices, but it appears according to my calculations that a different choice of submatrices will have to be made. We have shown how to determine whether a point lies on a line or in a plane, and we have shown whether two lines intersect, though we have not calculated their intersection point. Other remaining problems include finding the intersection of a line and a plane, calculating the plane defined by two lines, and computing the plane defined by a point and a line.