

Next: Essential and fundamental matrices
Up: Projective Geometry Applied to
Previous: Projective Geometry Applied to
Image formation involves the projection of points in
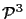 (the world) to points in
(the world) to points in
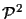 (the image plane). The perspective
projection equations with which we are familiar,
(the image plane). The perspective
projection equations with which we are familiar,
where the point (X,Y,Z) in the world is projected to the point (x,y)on the image plane, are inherently nonlinear. Converting to
homogeneous coordinates, however, makes them linear:
where
![$\ensuremath{{\bf p}} ' = [x,y,w]^T$](img135.gif) ,
,
![$\ensuremath{{\bf p}} = [X,Y,Z,W]^T$](img136.gif) ,
and
the perspective projection matrix T is given by:
,
and
the perspective projection matrix T is given by:
The entire image formation process includes perspective projection,
along with matrices for internal and external calibration:
![\begin{eqnarray*}\ensuremath{{\tilde P}} = T_{internal} T_{perspective} T_{exter...
...atrix{R & \ensuremath{{\bf t}} }\right] \nonumber \\
& = & A D,
\end{eqnarray*}](img138.gif)
(4)
where 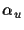 and
and 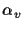 are the scale factors of the image plane
(in units of the focal length f),
are the scale factors of the image plane
(in units of the focal length f),
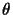 is the skew (
is the skew (
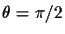 for most real cameras),
the point (u0,v0) is the principal point,
R is the
for most real cameras),
the point (u0,v0) is the principal point,
R is the
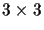 rotation matrix,
and
rotation matrix,
and
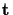 is the
is the
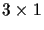 translation vector. The matrix A contains
the internal parameters and perspective projection, while D contains the
external parameters.
translation vector. The matrix A contains
the internal parameters and perspective projection, while D contains the
external parameters.
It is sometimes convenient to decompose the
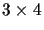 projection matrix
projection matrix
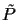 into a
into a
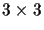 matrix P and a
matrix P and a
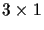 vector p
vector p
so that
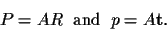 |
(5) |


Next: Essential and fundamental matrices
Up: Projective Geometry Applied to
Previous: Projective Geometry Applied to
Stanley Birchfield
1998-04-23
![]() (the world) to points in
(the world) to points in
![]() (the image plane). The perspective
projection equations with which we are familiar,
(the image plane). The perspective
projection equations with which we are familiar,
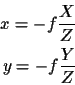
![\begin{displaymath}T_{perspective} = \left[\matrix{-f & 0 & 0 & 0 \cr
0 & -f & 0 & 0 \cr
0 & 0 & 1 & 0}\right].
\end{displaymath}](img137.gif)
![]() projection matrix
projection matrix
![]() into a
into a
![]() matrix P and a
matrix P and a
![]() vector p
vector p