Many interesting properties of molecular motion are best characterized statistically by considering an ensemble of motion pathways rather than an
individual one. For example, the "new view'' of protein folding kinetics replaces the traditional idea of a single folding pathway with the broader
notion of energy landscapes and folding funnels [Dill and Chan '97, Pande et al.
'98]. Proteins are thought to fold in a multi-dimensional funnel by following a myriad of pathways, all
leading to the same native structure. To carry out computational studies of molecular motion in this framework, we need efficient algorithms that can
quickly explore a large number of motion pathways. Unfortunately, classical simulation techniques such as Monte Carlo
methods [Kalos and Whitlock '86] and molecular dynamics [Haile '92] generate individual pathways one at a time and
are computationally inefficient if applied in a brute-force fashion to deal with many pathways. In this paper, we introduce
Stochastic Roadmap Simulation (SRS), a randomized technique for sampling molecular motion and
exploring the kinetics of such motion by examining multiple pathways simultaneously.
In Stochastic Roadmap Simulation, we compactly encode many motion pathways
with a directed graph called a probabilistic conformational roadmap, or just
roadmap for short. Every path in the roadmap is a potential motion pathway for the molecule. A roadmap thus contains many
pathways, with associated probabilities indicating the likelihood that a molecule may follow these pathways. By analyzing the paths represented in the
roadmap, we can efficiently obtain kinetic information on the motion of molecules over the entire energy landscape.

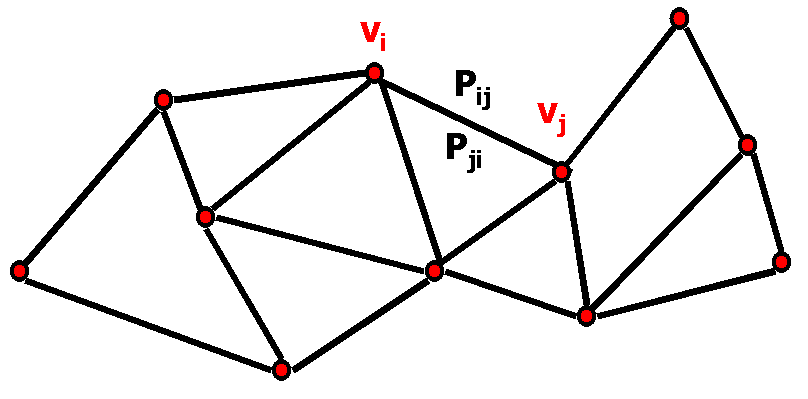
Figure 1: Example roadmap.
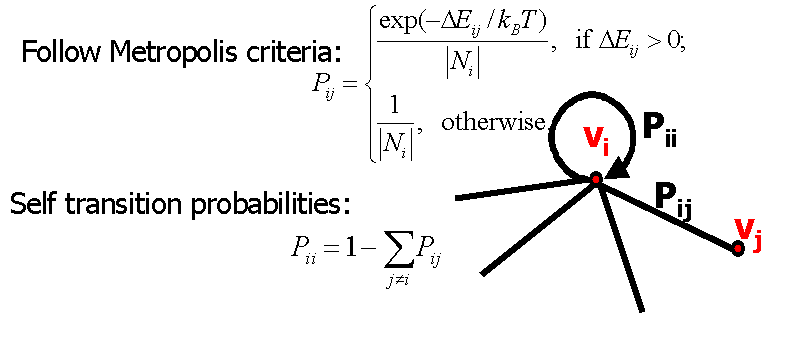
Figure 2: Edge probabilities on the roadmap.
As shown in Figure 1, each edge of our roadmap is associated with a probability
Pij. In comparison, previous work applying roadmap techniques to the
analysis of molecular motion used heuristic deterministic edge weights based on
energy differences [Singh et al. '99, Song and Amato '01, Apaydin et al. '01].
These heuristic approaches did not have a formal justification. On the other
hand, our edge probabilities are computed using the same Metropolis criteria
used in Monte Carlo (MC) simulation (Figure 2). With our new formulation,
every path in our roadmap corresponds to a particular Monte Carlo path.
Furthermore, we formally prove that Stochastic Roadmap Simulation
converges to the same limiting distribution as MC simulation.
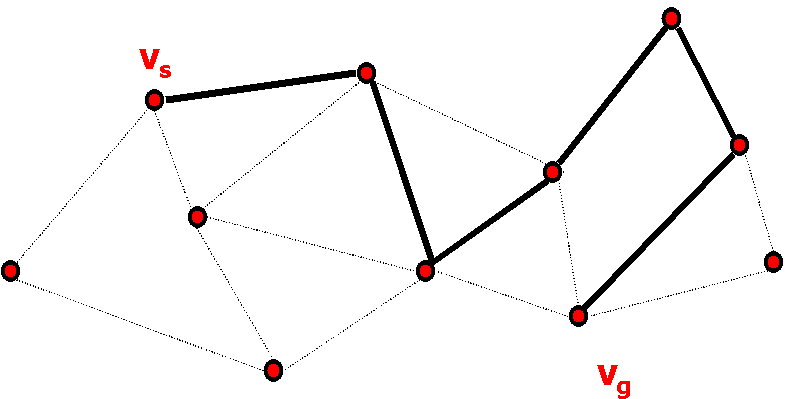
Figure 3: Sample path on the roadmap, corresponds to MC simulation path.
Our compact representation of stochastic molecular motion can be applied to the understanding of important biological processes, e.g., protein folding. A good example is the computation of the probability of folding (Pfold), i.e., for some starting conformation, the probability that a protein will reach the folded state before the unfolded state [Du et al. '98]. Pfold is an order parameter, giving an indication of how far a conformation is from the native structure. However, current approaches for computing Pfold require a large number of Monte Carlo or molecular dynamics simulations for each conformation, making the computation infeasible for more than a few starting states. On the other hand, using our Stochastic Roadmap Simulation approach we can efficiently compute Pfold for all conformations in the roadmap simultaneously. More specifically, we apply a convergent algorithm based on a tool from Markov Chain theory, first step analysis.
For empirical validation, we compared the Pfold computed by our SRS approach to results computed by MC simulation. Due to the computational cost of MC simulation, we could only generate MC-based Pfold estimates for a few starting states. Figure 4 shows correlation results for a hypothetical 2D energy landscape: The X axis indicates the number of nodes in the roadmap and the Y axis represents the correlation between the Pfold computed by SRS to the one computed by MC simulation for 100 starting conformations. The three curves indicate increasing number of MC simulations per starting conformation. The first observation is that the accuracy of the Pfold estimates computed by SRS improves as the roadmap size increases. The second, more interesting observation is that as number of MC simulations per starting conformation increases, the correlation increases. Thus, indicating that the Pfold estimates from SRS are better than the ones obtained by MC simulation.
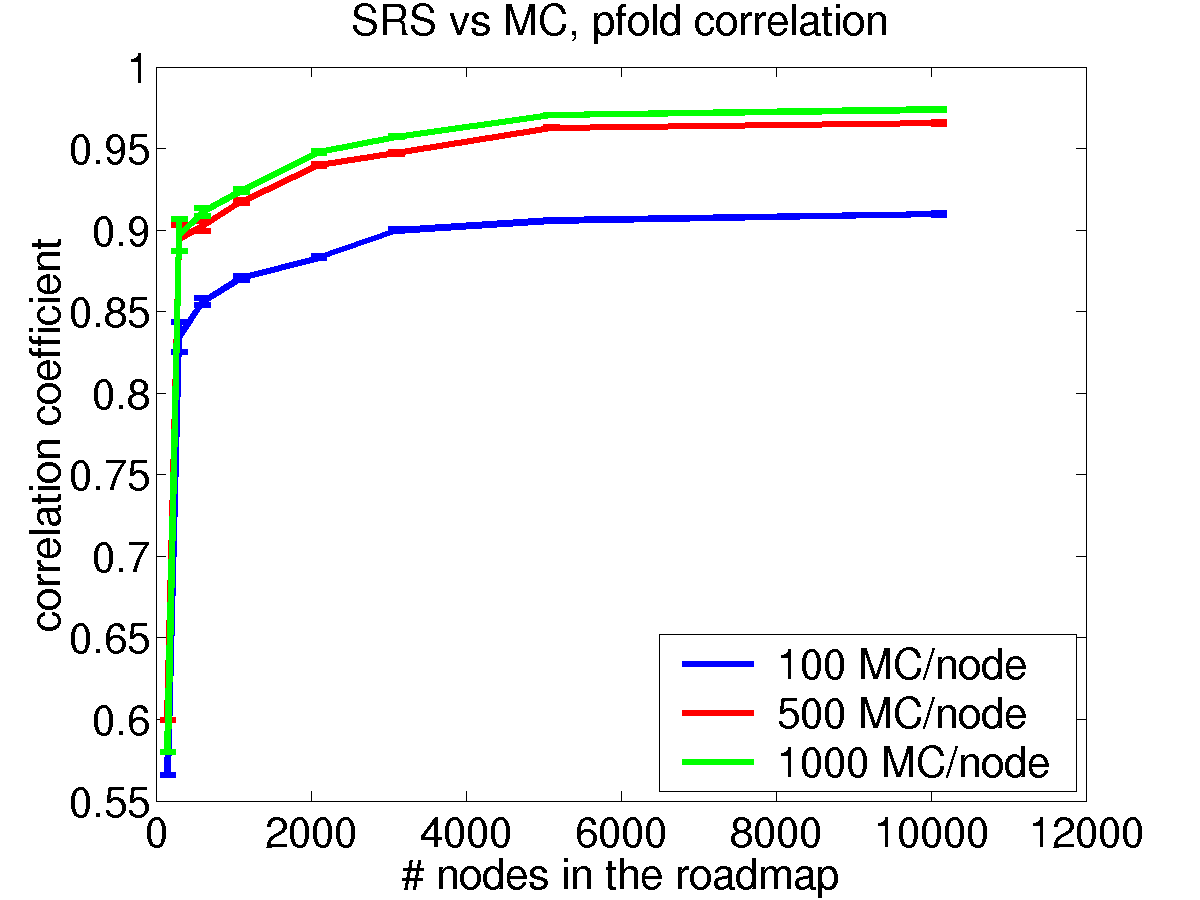
Figure 4: Correlation for Pfold computed by SRS against MC Simulation.
In terms of running time, our Stochastic Roadmap Simulation approach is much more efficient: Computing Pfold for all conformations in a roadmap of 10,000 nodes requires ~800 seconds of computing time and 10,000 energy computations. On the other hand, to estimate Pfold for only 100 conformations and 100 MC simulations per conformation requires 8077 seconds and ~220,000,000 energy computations. Note that Figure 4 suggests that MC results with only 100 simulations per node are very inaccurate.
In addition to the synthetic data, we also tested our algorithm on a real protein, repressor of primer (PDB ID 1ROP). 1ROP is a 4-helix
bundle. We study one monomer in isolation as in [Sun et al. '95]. We obtained the 3-D structure of 1ROP of the Protein Data
Bank. The monomer consists of 56 residues forming two alpha helices connected by
a loop. In our implementation, we specify the conformation of the monomer with a vector-based
representation [Singh and Brutlag '97, Apaydin et al '01]. The protein is represented by two vectors connected by a loop.
As in [Apaydin et al '01], there are six conformational parameters in total. Our energy function uses the
H-P model [Sun et al. '95] composed of two terms: one measuring the hydrophobic interaction and the other the excluded
volume. In our SRS and MC simulations, we discard self-colliding conformations. Here, the folded macrostate contains all conformations within 3
Å of the native fold according to the RMS distance, and the unfolded, all conformations
within 10 Å of the fully-extended conformation.
We studied the probability of folding for 1ROP for 36 randomly selected conformations. First, we
applied our SRS approach to compute estimates of the probability of folding for increasing roadmap sizes. For comparison, MC simulation was performed by starting from the
36 starting conformations. In MC simulation, the proposal conformation parameters were sampled uniformly in a radius of
15% of the original parameters. For every node, we performed up to 300 MC simulations. As in the synthetic case, we computed the correlation coefficient for increasing numbers of MC simulation. The results, shown in
Figure 5 suggest similar conclusions as in the synthetic case: First, the SRS estimates improve rapidly as the roadmap size increases. Second, the correlation tends to increase as we perform more MC simulations per node, hinting that variance in MC simulation estimates may be lowering the correlation values.
The total time to generate a roadmap with 5000 conformations and compute the probability of folding for all conformations in this roadmap was about one hour. On the other hand, for
one starting conformation running 300 MC simulations required, on the average,
three days of computation time, i.e., to generate the MC simulations for the plot in
Figure 5 we used about one hundred days of computation time, as opposed to the hour required for SRS for all 5000 nodes.
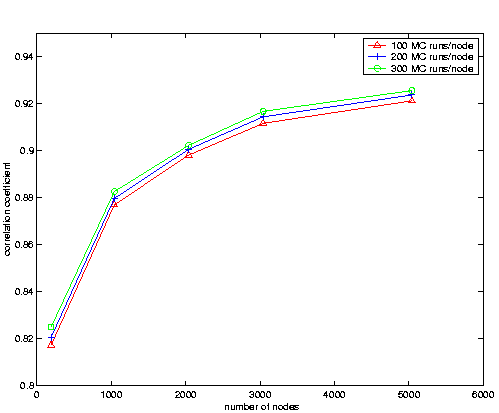
Figure 5: Comparison of Pfold computed by SRS to MC Simulation for 1ROP. We omitted error bars for clarity, for all points the standard error was at most 0.018.
In conclusion, we present a new representation for analyzing stochastic molecular motion. Our roadmap representation encodes many possible MC simulation paths into a compact graph structure. Such structure allows us to perform biologically relevant queries very efficiently. Furthermore, we formally proved that our roadmap approach converges to the same distribution as MC simulation. We presented the application of this paradigm to computation of the probability of folding, an important order parameter in protein folding. We obtained more accurate Pfold estimates than ones obtained by a conventional method, with a speed-up of many orders of magnitude. We are currently applying these concepts to the problem of ligand-protein docking.
| [Anfisen '73] - C.B. Anfinsen. Principles that govern the folding of protein chains. Science, 181:223--230, 1973. | |
| [Apaydin et al '01] - M.S. Apaydin, A.P. Singh, D.L. Brutlag, and J.C. Latombe. Capturing molecular energy landscapes with probabilistic conformational roadmaps. Proc. IEEE International Conference on Robotics and Automation, 2001. | |
| [Bryngelson et al '99] - J.D. Bryngelson, J.N. Onuchic, N.D. Socci, and P.G. Wolynes. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins: Structure, Function, and Genetics, 21(3):167--195, 1995. | |
| [Dill and Chan '97] - K.A. Dill and H.S. Chan. From levinthal to pathways to funnels. Nature Structual Biology, 4(1):10--19, 1997. | |
| [Dobson and Karplus '99] - C.M. Dobson and M. Karplus. The fundamentals of protein folding: Bringing together theory and experiment. Current Opinion in Structual Biology, 9:92--101, 1999. | |
| [Du et al '98] - R. Du, V. Pande, A.Y. Grosberg, T. Tanaka, and E. Shakhnovich. On the transition coordinate for protein folding. Jounal of Chemical Physics, 108(1):334--350, 1998. | |
| [Haile '92] - J.M. Haile. Molecular Dynamics Simulation: Elementary Methods. John Wiley & Sons, New York, 1992. | |
| [Kavraki et al. '96] - L. Kavraki, P. Svestka, J. C. Latombe, and M. H. Overmars. Probabilistic roadmaps for path planning in high-dimensional configuration space. IEEE Transactions on Robotics and Automation, 12(4):566--580, 1996. | |
| [Kalos and Whitlock '86] - M.H. Kalos and P.A. Whitlock. Monte Carlo Methods, volume 1. John Wiley & Son, New York, 1986. | |
| [Pande et al. '98] - V.S. Pande, A.Y. Grosberg, T. Tanaka, and D.S. Rokhsar. Pathways for protein folding: Is a new view needed? Current Opinion in Structual Biology, 8:68--79, 1998. | |
| [Song and Amato '01] - G. Song and N.M. Amato. Using motion planning to study protein folding pathways. Proc. ACM Int. Conf. on Computational Biology (RECOMB), pages 287--296, 2001. | |
| [Singh and Brutlag '97] - A.P. Singh and D.L. Brutlag. Hierarchical protein structure superposition using both secondary structure and atomic representations. In Proc. Int. Conf. on Intelligent Systems for Molecular Biology, pages 284--293, 1997. | |
| [Singh et al '99] - A.P. Singh, J.C. Latombe, and D.L. Brutlag. A motion planning approach to flexible ligand binding. Proc. Int. Conf. on Intelligent Systems for Molecular Biology, pages 252--261, 1999. | |
| [Sun et al. '95] - S.~Sun, P.D. Thomas, and K.A. Dill. A simple protein folding algorithm using a binary code and secondary
structure constraints. Protein Engineering, 8:769--778, 1995. |