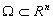is a function which satisfies
the laplace's equations:
This work has been been submitted as a term paper in the course: Robot Motion Planning (ME766, Instructor: Dr. Bhaskar Dasgupta).
In this term paper we attempt to do Path Planning by generating local minima free Potential Function values for given Work-cells. These functions are the solutions of the Laplace's equation and are called harmonic functions. These functions are complete (up to discretization error), analytic and free from spurious local minimas. Though generation of such functions is computationally very expensive, yet they can be used for real time navigation by pre-generating a database of such functions for all possible goal points in a given Workcell.
Potential field methods, introduced by Khatib [1], are widely used for real time collision free Path Planning. The attraction of a Potential Field method is its being a fastest optimization procedure. However such functions are usually plagued by local minimas. That is the robot may get stuck at a local minima before attaining the goal configuration.
The issue can be addressed at two levels:
1.In definition of potential function by specifying a function with no or few local minima.
2.In the design of search algorithm , by including the appropriate techniques for escaping from local minima
" So the need is to find potential function with no or few local minima and by using it to develop a path planning method"
Laplace's Equations, along with appropriate boundary conditions, are solved to get the desired navigation Functions.
In 1990 Connolly [2] proposed the use of local minima free Harmonic Functions for Path Planning .
A harmonic function is on a domain 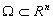is a function which satisfies
the laplace's equations:
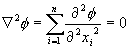
Harmonic functions satisfy the min-max principle: spontaneous creation of local minima within the region is impossible if laplace's equation is imposed as constraint on the function used.
So if a function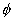 
satisfies the laplace's equation on some region 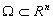, then 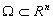attains its minimum and
maximum values only on the boundary 
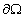of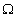 
.
Any critical points of the function in the interior of this region must be saddle points, since local extrema of the function are not possible there.
If the effector reaches a saddle point, and it is not near the goal, then there must be a way out. The exit from this critical point can be found out by performing a search in the neighborhood of the critical point.
Though Harmonic Functions are free from local minimas, they are not fully Global. Using the Poincare-Hopf theorem Koditschek [3] showed that in the presence of C-obstacles, a global navigation function does not exist in general. For a two dimensional C-space with q disjoint C-obstacles, each homeomorphic to a closed unit disc, a potential function U must possess at least q saddle points.
Boundary Conditions are required for solving the Laplace's equations. Any of the following two boundary conditions can be used:
If 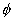is
the harmonic function and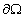
represents the boundary of the C-obstacles, then the Dirichlet boundary
condition is:
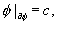
where c is a constant. In this case the boundary is held fixed at a particular potential. Since the boundary conditions are fixed, the flow must be along the outward normal of the obstacle surface. The gradient of the harmonic solution, therefore, tends to depart from C-space obstacle boundaries.
Neumann boundary conditions are described by:
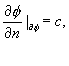
where c is a constant and is usually fixed to 0 so that the flow is tangential to the obstacle. But the tangential-flow behavior exhibited by a Neumann solution can result in a tendency for a robot to stay close to C-space obstacle surfaces.
If f d represents the solution obtained from Dirichlet boundary conditions and f n represents the solution obtained from Neumann boundary conditions, then a new harmonic function can be constructed by taking the linear combination of the two:
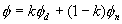,where k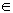 
[0, 1]. This composition preserves the harmonic solutions to obtain a harmonic
constraint and therefore guarantees no local minima and collision-free paths.
If k < 0.5, then shallow gradients found in the Dirichlet solution can be avoided.
If a path between the current state and the goal exists, then it will be found using this formulation.
Numerical solutions for laplace's equation have been obtained from finite
difference methods. Let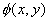 
be the function which satisfies the , and let 
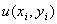represent a discrete regular
sampling of 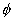on a grid. A
central difference formula for the second derivatives of 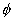are:
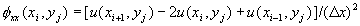
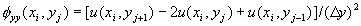
where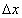 
: step size in
x-direction and,
: step size in
y-direction.
This is a second order accurate scheme.
If 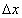= = h then laplace's equation in
discrete form:
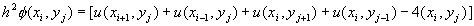
The easiest way to solve a laplace's equation is to solve another equation which give the same solution at the steady state. We use a "parabolic type equation" :
This is an unsteady analog which gives the as the steady state.
Finite difference in time/central difference in space:
For
Using this condition we get
which gives
So we start from some arbitrary initial field and time step according to the
formula for finding the interior points.
At this point we use the two boundary conditions (Dirichlet
boundary condition and Neumann boundary condition) as discussed previously to
specify the 'u' value at boundary points at each time step.
1. Assume a field and the initial values of 2. Using formula
we get the 3.Using boundary conditions we get the 4. If || Else This method is easily extendable to 3-D and higher dimensions.
Once the array u has been computed to necessary precision, path
can be computed simply by following the gradient from the starting point. The
path must end at the goal point (or set) .
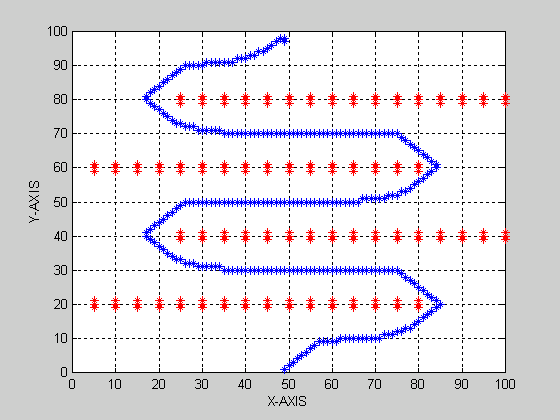
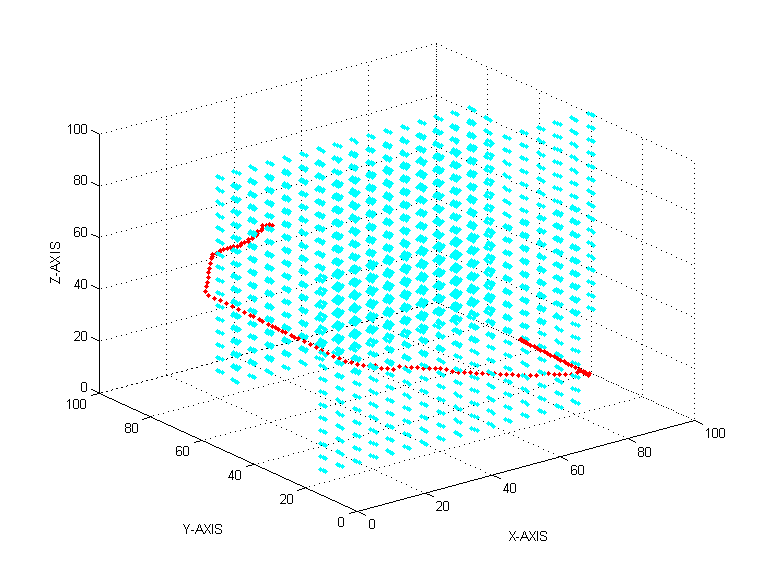
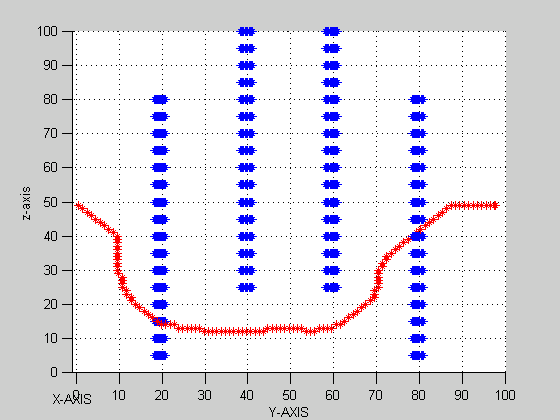
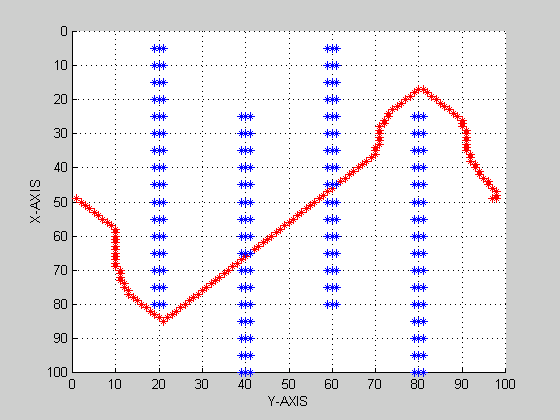
PROBLEM-1 (IN 2-D) Using Dirichlet Boundary Condition PROBLEM-1 (IN 2-D) Using Neumann Boundary Condition PROBLEM-2 (IN 2-D) Using Dirichlet Boundary Condition PROBLEM-2 (IN 3-D) Using Dirichlet Boundary Condition PROBLEM-2 (IN 3-D) PROJECTION IN Y-Z PLANE
PROBLEM-2 (IN 3-D) PROJECTION IN X-Y PLANE
PROBLEM-1 (IN 3-D) Using Dirichlet Boundary Condition PROBLEM-1 (IN 3-D) PROJECTION IN X-Z PLANE
Harmonic functions worked out for the cases shown, were free
from local minimas. All paths starting from the initial point led to the goal
point. However following problems were observed while working out the cases
shown:
As compared to other Potential field methods, this is
computationally very expensive, and becomes unmanageable for larger grid size
and higher dimension. It took hours to get results for the 3-D cases. In the case of Dirichlet boundary conditions, many patches
with nearly zero values of |Ñ f | were found in the Cfree as seen the
following f (harmonic solution from laplace's equation) plot for thfirst 2-D
case shown in the results.
While Neumann conditions give better navigation functions as
is clear from the following plot of f for the same case:
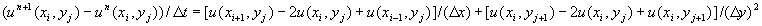
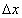= and using the condition for
"numerical stability" i.e.
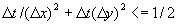
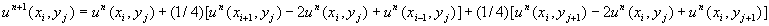
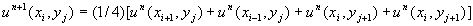
For the boundary points:
Algorithm :
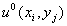at each of the node points.
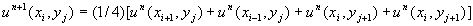
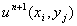values at
each interior points.
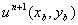values at each boundary point.
- 
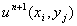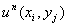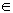|| < = , STOP (where 
)
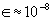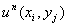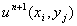= and GO TO step-2
Results:
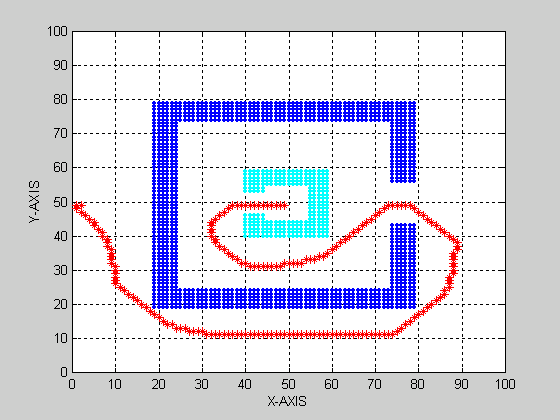
(Grid
Size=100x100 , Sink f =-108 , Boundary f = 1)
( Accuracy = 10-4 , Total
Iterations = 647 )
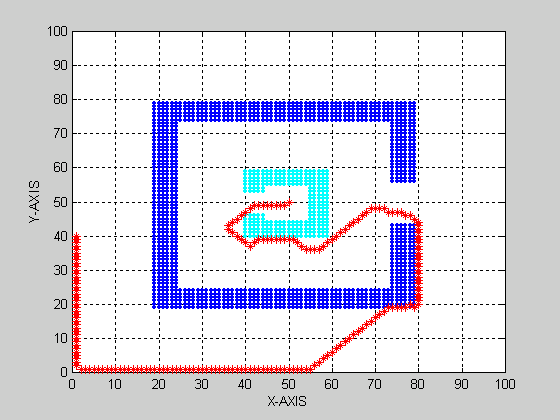
(Grid Size=100x100
, Sink f =-0.5 )
( Accuracy = 10-6 , Total Iterations =7485 )
(Grid
Size=100x100 , Sink f =-108, Boundary f = 1)
( Accuracy = 10-5 , Total
Iterations = 573 )
(Grid
Size=100x100x100, Sink f =-108, Boundary f = 1)
( Accuracy = 10-5 , Total
Iterations = 1278 )
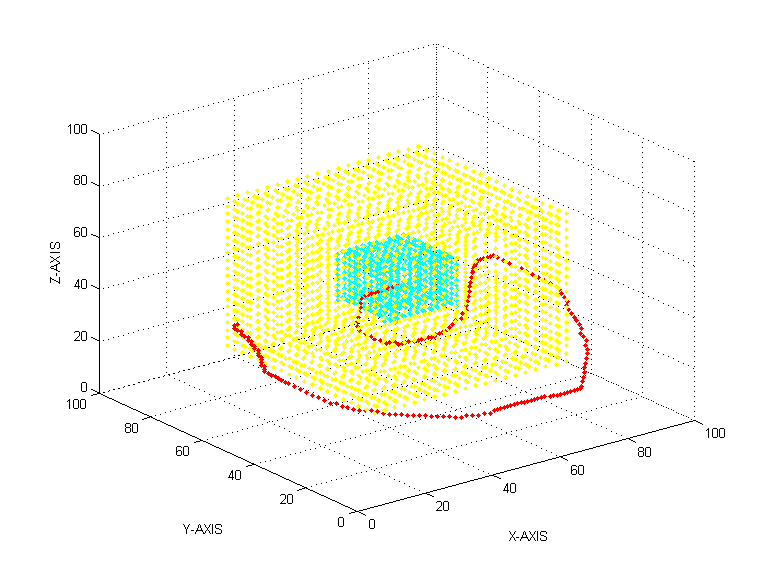
(Grid
Size=100x100x100 , Sink f =-108, Boundary f = 1)
(Accuracy = 10-6 , Total
Iterations = 2138)
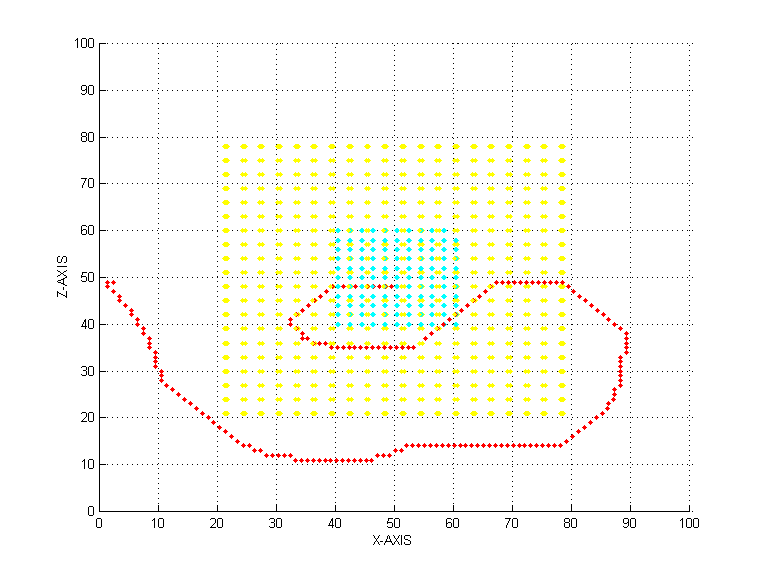
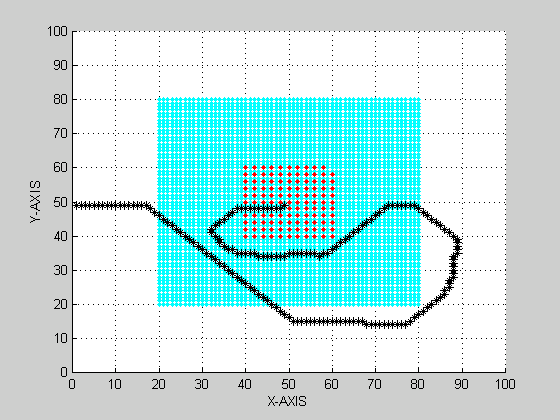
PROBLEM-1 (IN 3-D) PROJECTION IN X-Y PLANE
Inferences
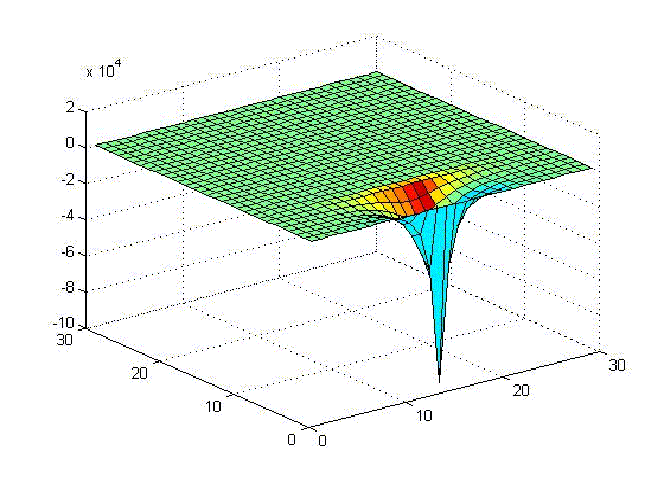
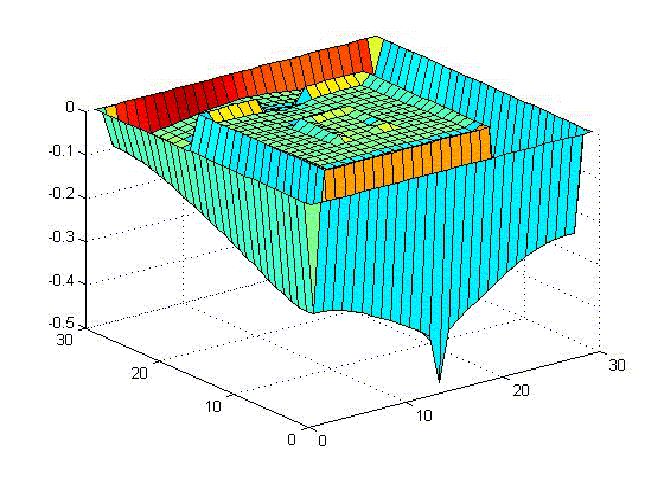
Neumann boundary conditions causes the robot to graze past
the obstacles in their way to the goal (as shown in Results: Problem 1,
Neumann boundary conditions).
Inspite of the above problem, for higher dimensions and higher grid size, Dirichlet boundary conditions give more convincing results than Neumann boundary conditions.
Though free from local minimas, the charm of such potential
functions would be lost if its computation cost hinders its on-line application.
However one can see that for a given configuration space and a goal point,
harmonic functions are same for all starting points in the configuration space.
This fact can be used for online navigation. For this one has to maintain a
database of harmonic functions for all possible goal points. Thus during
navigation, when the goal point is usually fixed, one can initially(when the
goal point is set) access the harmonic function corresponding to that goal point
from the database and use it throughout to navigate from any point in the
C-space to the goal point using a steepest descent search routine.