 (23MB)
(23MB)
 (5MB)
(5MB)
Please take a look at these videos:
 (23MB)
(23MB)
 (5MB)
(5MB)
Other pages: Global Dynamic Window Decomposition-based Motion Planning Homepage
Algorithms for motion generation can be divided into two main groups: motion planning algorithms and reactive motion execution algorithms. With few exceptions, almost all algorithms presented in the robotics literature fall into one of these categories.
Motion planning algorithms make the assumption that everything about the environment is known at planning time. Most of them actually assume that the world will not change in the future, implying that all obstacles are static. Some of them allow for moving obstacles, but only if the motion of all non-stationary obstacles is known as a function of time.
To generate a motion those algorithms build a representation of the obstacles in the configuration space of the robot. The configuration space is the space describing all possible positions or configurations of the robot. If a particular configuration, described using the position of all the joints of the robot, is in collision with the environment, it does not correspond to a physically possible configuration. This point is considered to be part of a configuration space obstacle, a set of inadmissible configurations. If we are dealing with robots with many joints, the configuration space is high-dimensional and the computation of configuration space obstacles, or even approximations to it, is computationally very costly and can take from multiple seconds to hours. Planning algorithms that also allow for obstacles moving on a known trajectory augment the configuration space with another dimension: time. A configuration space obstacle in configuration-time space is a configuration space obstacle sweeping along the time axis. Motion planning is performed by finding a continuous curve connecting the initial and the final configuration of the robot. Sounds simple, but it can get pretty complex.
This all works fine until an unforeseen obstacle appears, or a known obstacle does not move as it was assumed during planning. Now the motion generated by the motion planning algorithm might not be valid any more. The environment has changed and the assumptions that lead to that particular motion do not hold any more. The solution is to plan a new motion from scratch, given the new information about the environment. If a robot is supposed to accomplish a task in a space that changes frequently, however, this is not practical any more. Unless you find it desirable that a robot moves for an inch, discovers an unforeseen obstacle, stops, plans for a couple of seconds or hours, moves for an inch and so on...
So, while incredible progress has been made in motion planning over the last few years - in particular with randomized approaches and researchers have gained a thorough practical and theoretical understanding of the domain, the problem of motion generation in highly dynamic and unstructured environments remains.
Reactive algorithms take a very different approach. Rather than translating the entire world into configuration space to find a motion, they just take the immediate surroundings of the robot into account. The robot tends to move towards the goal, unless an obstacle is in the way. The most famous approach is the potential field approach first introduced by Khatib. The robot is drawn towards to the goal by virtual attractive forces. Obstacles exert a virtual repulsive force on the robot. These forces guide the robot to the goal - unless the robot gets stuck in a local minima. A local minima is configuration of the robot at which attractive and repulsive forces result in total force of zero: the robot stops although it has not reached the goal yet.
Many other similar approaches have been developed. They are either susceptible to local minima, or require global computation, which can get computationally as complex as motion planning itself. I'll mention one: The attractive and repulsive forces mentioned above can be defined in many different ways. For example, you could imagine that the entire world is filled with water and there is a sink at the goal. Eventually all water is going to flow into the sink. If you trace the flow of the water molecules you will obtain what is called a local minima-free potential function. Following the gradient of this function is guaranteed to lead you to the goal. Unless, of course, the environment changes, at which point you have to fill up the environment with water again. You can imagine that computing the fluid dynamics, even with simplified assumptions, is a difficult task, in particular for arbitrarily shaped obstacles. Then we are back to moving for a little bit, computing a motion for a long time, and moving a little bit.
To sum up: Motion planning algorithms are great because they can guarantee the robot to reach the goal - local minima are not an issue. But they are slow. Reactive approaches to motion generate are fast, they work well in highly dynamic environments, but the robot might not reach the goal. The elastic strip framework attempts to combine motion planning and reactive execution to have the best of both worlds: goal-directed motion in unpredictably changing environments. And all this for robots with many degrees of freedom, because that's what is needed to execute complicated tasks.
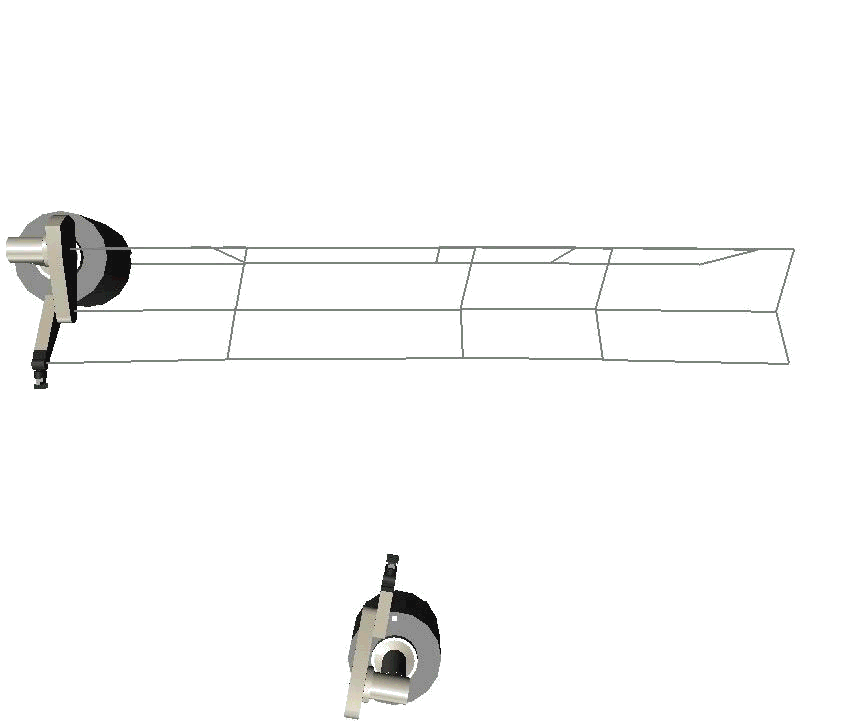
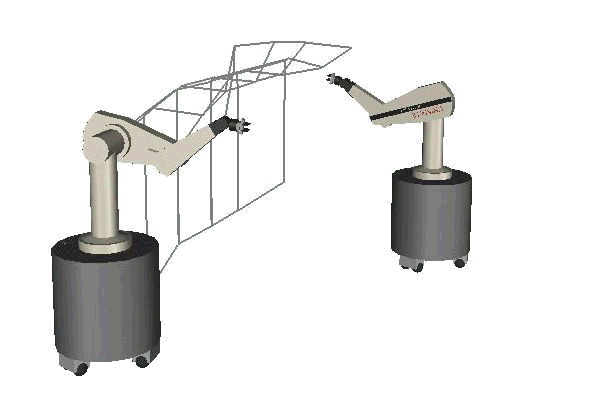
The following three images illustrate how the elastic strip framework accomplishes that. A path, previously generated by a motion planner, is represented as a "strip" of elastic material in the workspace. Such a strip can be generated by connecting certain control points on consecutive configurations along the path. In the images the strip is indicated as a gray wire frame connected to the robot on the left.
The robot itself is SAMM - the Stanford Assistant Mobile Manipulator, a mobile manipulator with nine degrees of freedom, consisting of a holonomic mobile base with three degrees of freedom and a PUMA 560 manipulator arm with six degrees of freedom. It can operate a couple of hours unteathered and has two Pentium PCs onboard.
|
|
|
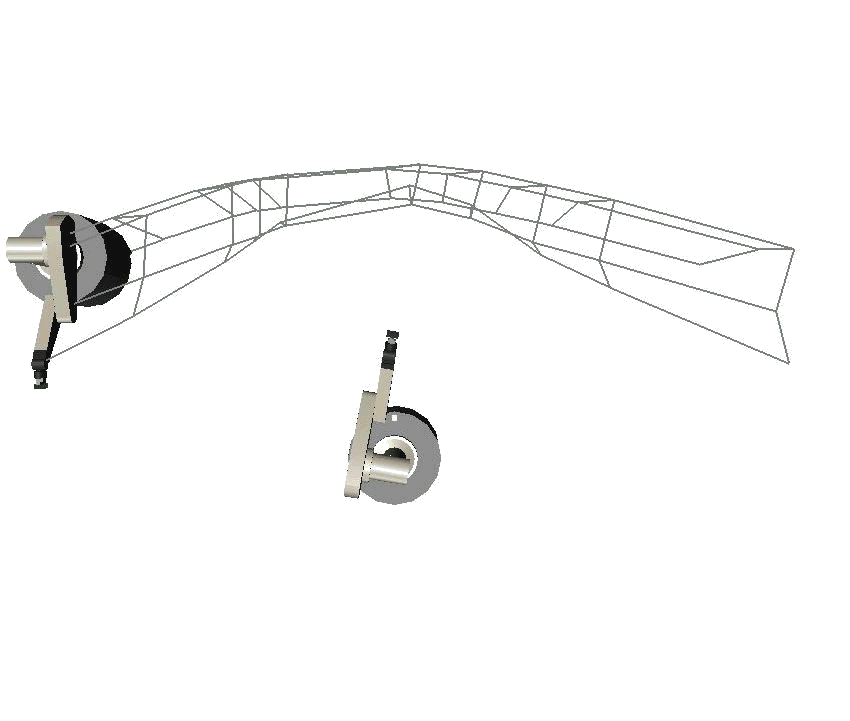
The images illustrate how a second SAMM acts as a moving obstacles and moves into the trajectory of the robot to the left. The trajectory is modified in real time in order to avoid the obstacle. Note how the trajectory is always connected to the goal configuration. This guarantees that the goal configuration is reached, if at all possible. Of course, if an obstacle moves onto the goal configuration we cannot move our robot there...
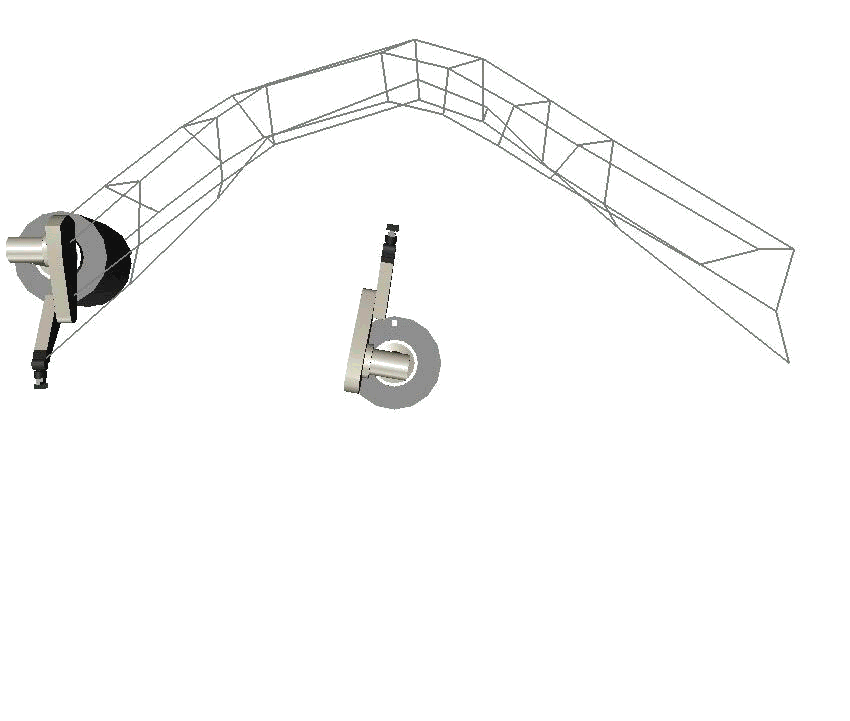
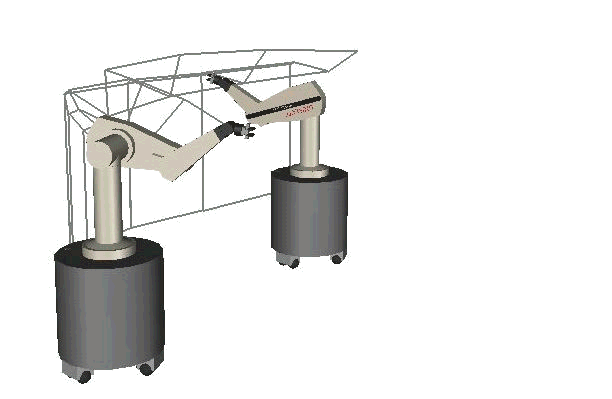
The second series of three images shows the same experiment, but from a different perspective. Is interesting to observe from this perspective that all degrees of freedom of the robot are used to avoid the obstacle: the arm bends its elbow and shoulder - in addition to the base following a curved trajectory, instead of a straight one. You can see this by looking at the wire frame. The grid lines indicated the general posture of the robot.
|
|
|
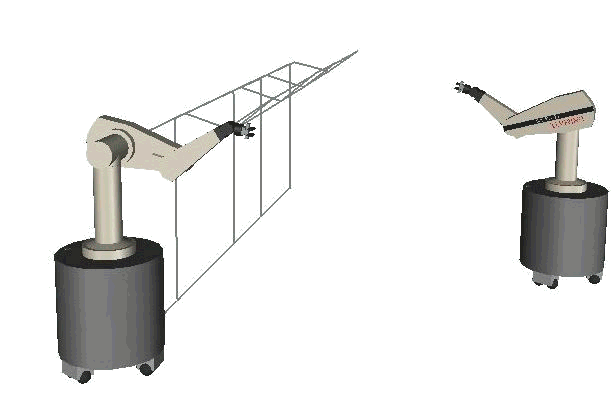
The final set of images shows again the same experiment, but this time using real robots. These two SAMMs are called Romeo and Juliet. Sensing, which is an important aspect of motion generation is not addressed in this particular work. The obstacle robot communicates with the other one to transmit its current location. Now the elastic strip program can update its world model and modify the strip accordingly. A couple of ideas for sensing are briefly discussed in my thesis (PDF 3.7MB or PS 15MB) and will be part of my future research. A video exists of these experiments, but unfortunately only on VHS.

|

|

|
You will be able to find a lot of detail about the elastic strip framework and various applications, for example in a multi-robot work cell, in the publications below. A key aspect of it is obviously monitoring the free space around the current trajectory. If the free space shrinks, an obstacle is approaching and the elastic strip has to be changed. The interesting part is that very simple potential field-based approaches can be used for this modification. The resulting forces are simply mapped into joint space, using the Jacobian of the manipulator. This makes this approach computationally very efficient and applicable to robots with many degrees of freedom. The experiments I've made use up to eleven degrees of freedom, but they also indicate that many more would be computationally feasible.
There are two kinds of forces acting on elastic strip: Repulsive forces are computed as a function of distance from obstacles and translate into displacement of the elastic material. In addition, there are internal forces acting, which cause the elastic to shorten when an obstacle retracts again.
The elastic strip approach has a couple of other interesting properties. In contrast to motion planning algorithms, it actually generates a trajectory (a time-parameterized path), rather than just a path. It can incorporate various dynamic properties of the robot while generating the motion. This allows for more robust and efficient motion, fully utilizing the capabilities of the robot.
The way the forces acting on the elastic strip are translated into joint torques allows for the integration of task behavior and obstacle avoidance behavior. An example: using the elastic strip approach, a robot could inspect an overhead gas pipe with a camera, while the base zig-zags around obstacles on the ground. The obstacle avoidance motion can be mapped into the Nullspace of the manipulator's Jacobian, such that it does not affect the motion of the end-effector or camera. All of this is happening in real time in reaction to obstacles, as the robot moves along.
Below are three videos demonstrating this kind of behavior, which resulted from work together with Sriram Viji: on the left the elastic strip is used to avoid obstacles, but the task is not maintained. The video in the middle shows how task execution and obstacle avoidance can be integrated. The task is to follow the red line with the end effector. Watch how in the first video the end effector deviates significantly from the task so that the obstacles can be avoided. In the second video the end effector does not deviate at all, despite the fact that the obstacles perform the same motion as in the first video.
Sometimes constraints can make it impossible to perform the task. In the case of the third video, the end effector has to deviate from the task to avoid the second Scout robot. The framework allows task suspension and automatic task resumption; watch closely, how the end effector deviates from the line and after passing the obstacle resumes the task.
Click on the images to see the movies.
You can also check out our video submission to ICRA 2002: Task-Consistent Obstacle Avoidance for Mobile Manipulation (23MB)
One of the most frequent questions about the elastic strip framework is the following: What happens when an obstacle crosses the path and just keeps moving? Doesn't the elastic strip framework then generate very suboptimal paths? There is a long answer to this question, dealing with the division between planning and execution. Fortunately, there also is a short one, because elastic strips allow a very natural way to deal with this problem. We call it local replanning. A topologically different path is generated by following simple potentials: external forces can push adjacent configurations apart so that obstacles can pass trought it. Since this is a local method it can fail, but in practice it solves many problems. By maintaining two strips, one which lets the obstacle pass and one which doesn't, most cases can be addressed. The video below gives an example of an obstacle passing through the strip.
Click on the image to see the movie.
Ultimately, though, a planner might have to be invoked to guarantee an optimal trajectory. That's why I would like to integrate the elastic strip framework with decomposition-based planning.
In the following two videos you see the elastic strip approach applied to a humanoid robot with more than 30 degrees of freedom. This is a fairly complicated environment, in which one of the office chairs moves into the path of the robot and the upper beam of the door is lowered during the motion. The left video shows how the robot moves without posture control. The video on the right shows the same motion when a very simple posture behavior is imposed. It does not look perfectly human yet, but it serves well to illustrate the idea and the ease with which such posture can be integrated in the elastic strip framework. In the future, we will work on postures based on balance constraints and so on...
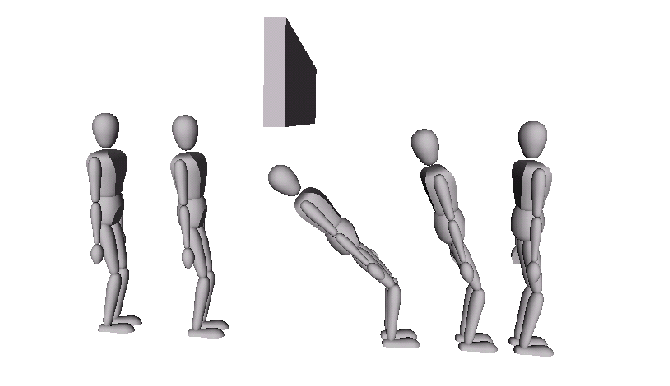 without posture (1MB)
without posture (1MB)
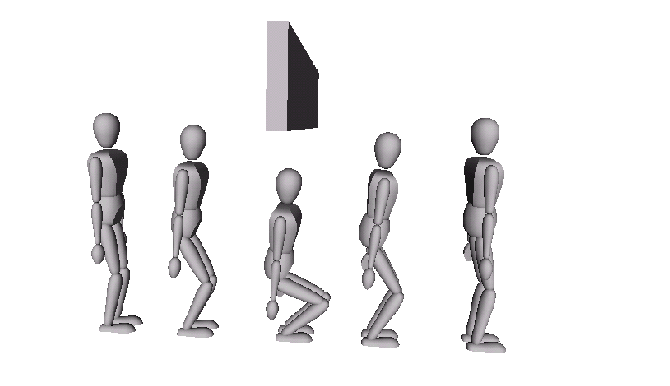 with posture (1MB)
with posture (1MB)
 without posture (6MB)
without posture (6MB)
 with posture (6MB)
with posture (6MB)
And here is another (slightly humorous) video, showing a humanoid robot skiing. The serious point here is to show how all degrees of freedom are used in real time to avoid obstacles. Watch how the snowman moves into the path and how the finish sign is sliding down the poles. Note how the ski poles move to avoid the snowman and to fit through the finish gate; note also how the whole posture of the robot changes to pass under the finish sign.
Elastic strips and decomposition-based motion planning are versatile frameworks that will find application in many domains beyond robotics, like virtual prototyping, character animation, haptic display of virtual environments, multi-robot workcells, and molecular biology. The ability to generate motion for multi-link objects in dynamic environments is a big challenge in those areas, which can be addressed using these approaches.
Looking at the skiing video, for example, you can imagine how these methods find direct applicability in character animation for movies or video games. The motion of characters can be specified independently of other characters or objects in the scene, and independently of the number of degrees of freedom at the task level. This allows for more realistic games with higher interactivity for smaller production costs.
| Visitors since February 1, 2002: | provided by |