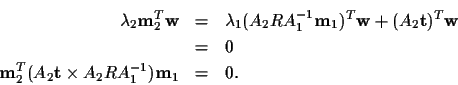

Next: Alternate derivation: from the
Up: Essential and fundamental matrices
Previous: Essential and fundamental matrices
To describe the relationship between R,
 ,
A1, and A2 more
exactly, and to connect the above equations with those found in
[6], we offer the following algebraic derivation.
,
A1, and A2 more
exactly, and to connect the above equations with those found in
[6], we offer the following algebraic derivation.
Recall that a point
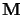 produces an image
produces an image
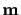 through the equation
through the equation
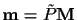 .
Without loss of generality, we can assume that
.
Without loss of generality, we can assume that
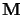 is given
with respect to the first camera's coordinate frame to yield the following
two imaging equations:
is given
with respect to the first camera's coordinate frame to yield the following
two imaging equations:
where 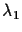 and
and 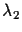 are scale factors,
are scale factors,
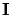 is the
is the
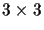 identity matrix and
identity matrix and
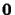 is the
is the
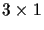 null
vector. By letting
null
vector. By letting
![$\ensuremath{{\bf M}} = \left[\matrix{\ensuremath{{\bf\hat M}} ^T & 1}\right]^T$](img170.gif) (
(
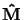 is
is
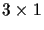 ), we
achieve the following relation:
), we
achieve the following relation:
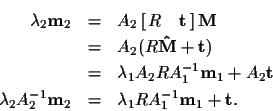
(8) (9)
Geometrically, this equation says that the vector on the left is a linear
combination of the two vectors on the right. Therefore, they are all
coplanar, and the vector
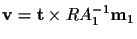 is perpendicular to that plane:
is perpendicular to that plane:
which is identical to (6).
Similarly, the vector
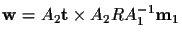 is perpendicular to the vectors in (8):
is perpendicular to the vectors in (8):
This is a surprising result because it gives us a new and equivalent
expression for F:
![\begin{displaymath}F =[A_2 \ensuremath{{\bf t}} ]_x A_2 R A_1^{-1},
\end{displaymath}](img177.gif) |
(10) |
which shows that F can be written as the product of an
anti-symmetric matrix
![$[A_2 \ensuremath{{\bf t}} ]_x$](img178.gif) and an invertible matrix
A2 R A1-1 [4].
and an invertible matrix
A2 R A1-1 [4].


Next: Alternate derivation: from the
Up: Essential and fundamental matrices
Previous: Essential and fundamental matrices
Stanley Birchfield
1998-04-23
![]() ,
A1, and A2 more
exactly, and to connect the above equations with those found in
[6], we offer the following algebraic derivation.
,
A1, and A2 more
exactly, and to connect the above equations with those found in
[6], we offer the following algebraic derivation.
![]() produces an image
produces an image
![]() through the equation
through the equation
![]() .
Without loss of generality, we can assume that
.
Without loss of generality, we can assume that
![]() is given
with respect to the first camera's coordinate frame to yield the following
two imaging equations:
is given
with respect to the first camera's coordinate frame to yield the following
two imaging equations:
![\begin{eqnarray*}\lambda_1 \ensuremath{{\bf m}} _1 & = & A_1 \left[\matrix{\ensu...
...matrix{R & \ensuremath{{\bf t}} } \right] \ensuremath{{\bf M}} ,
\end{eqnarray*}](img165.gif)
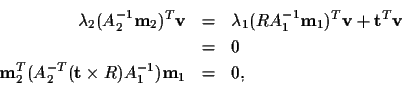
![]() is perpendicular to the vectors in (8):
is perpendicular to the vectors in (8):