Suppose we have a point (x,y) in the Euclidean plane.
To represent this same point in the projective plane, we simply add a
third coordinate of 1 at the end: (x, y, 1).1
Overall scaling is unimportant, so the point (x,y,1) is the same as the
point
![]() ,
for any nonzero
,
for any nonzero ![]() .
In other
words,
.
In other
words,
To represent a line in the projective plane, we begin with a standard
Euclidean formula for a line
| aX+bY+cW | = | 0 | |
| = | 0, | (1) |
To transform a point in the projective plane back into Euclidean
coordinates, we
simply divide by the third coordinate:
(x,y) = (X/W, Y/W). Immediately
we see that the
projective plane contains more points than the Euclidean plane,
that is, points whose third coordinate is zero. These points
are called ideal points, or points at infinity. There is a
separate ideal point
associated with each direction in the plane; for example, the points
(1,0,0) and (0,1,0) are associated with the
horizontal and vertical directions,
respectively. Ideal points are considered just like any other point
in
![]() and are given no special treatment.
All the ideal points lie on a line, called the ideal line, or
the line at infinity, which, once again, is treated just the same as
any other line. The ideal line is represented as (0,0,1).
and are given no special treatment.
All the ideal points lie on a line, called the ideal line, or
the line at infinity, which, once again, is treated just the same as
any other line. The ideal line is represented as (0,0,1).
Suppose we want to find the intersection of two lines.
By elementary algebra, the two
lines
![]() and
and
![]() are found to
intersect at the point
are found to
intersect at the point
![]() .
This formula is more easily
remembered as the cross product:
.
This formula is more easily
remembered as the cross product:
![]() .
If the two lines are parallel, i.e.,
-a1/b1 = -a2/b2, the point of
intersection is simply
(b1c2-b2c1,a2c1-a1c2,0), which is the
ideal point associated with the direction whose slope is -a1/b1.
Similarly, given two points
.
If the two lines are parallel, i.e.,
-a1/b1 = -a2/b2, the point of
intersection is simply
(b1c2-b2c1,a2c1-a1c2,0), which is the
ideal point associated with the direction whose slope is -a1/b1.
Similarly, given two points
![]() and
and
![]() ,
the
equation of the line passing through them is given by
,
the
equation of the line passing through them is given by
![]() .
.
Now suppose we want to determine whether three points
![]() ,
,
![]() ,
and
,
and
![]() lie on the same line. The line joining the first two points
is
lie on the same line. The line joining the first two points
is
![]() .
The third point then lies on the line if
.
The third point then lies on the line if
![]() ,
or, more succinctly, if the
determinant of the
,
or, more succinctly, if the
determinant of the
![]() matrix containing the points is zero:
matrix containing the points is zero:
Example 1. Given two lines
![]() and
and
![]() ,
the point of intersection is given by:
,
the point of intersection is given by:
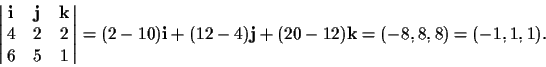
Example 2. Consider the intersection of the hyperbola xy=1 with the horizontal line y=1. To convert these equations to homogeneous coordinates, recall that X=Wx and Y=Wy, yielding XY=W2 for the hyperbola and Y=W for the line. The solution to these two equations is the point (W,W,W), which is the same as the point (1,1) in the Euclidean plane, the desired result. Now let us consider the intersection of the same hyperbola with the horizontal line y=0, an intersection which does not exist in the Euclidean plane. In homogeneous coordinates the line becomes Y=0 which yields the solution (X,0,0), the ideal point associated with the horizontal direction.